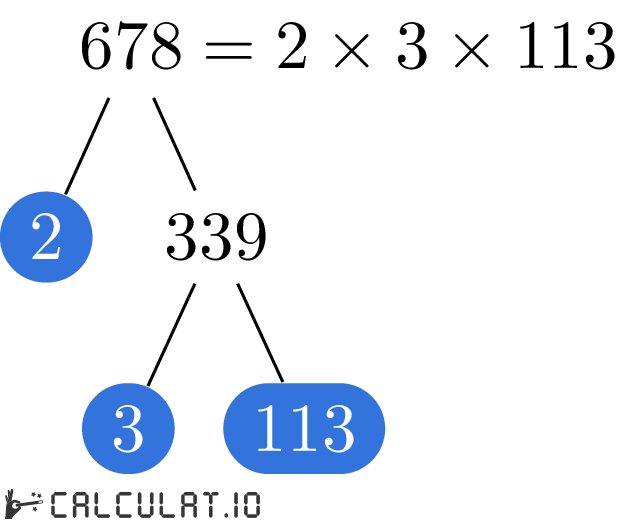
Разложение числа 678 на простые множители
Какие простые множители у числа 678?
Объяснение разложения числа 678 на простые множители
Разложение 678 на простые множители (факторизация) - это представление числа 678 как произведения простых чисел. Другими словами, необходимо выяснить, какие простые числа нужно перемножить, чтобы получилось число 678.
Так как число 678 является составным (не простым) мы можем разложить его на простые множители.
Для того, чтобы получить список простых множителей числа 678, необходимо итеративно делить число 678 на минимально возможное простое число пока в результате не получится 1 (единица).
Ниже полное описание шагов факторизации числа 678:
Минимальное простое число на которое можно разделить 678 без остатка - это 2. Следовательно, первый этап расчета будет выглядеть следующим образом:
678 ÷ 2 = 339
Теперь необходимо повторять аналогичные действия, пока в результате не останется 1:
339 ÷ 3 = 113
113 ÷ 113 = 1
В итоге мы получили список всех простых множителей числа 678. Это: 2, 3, 113
Дерево простых множителей числа 678
Мы также можем визуализировать разложение числа 678 на простые множители в виде дерева факторизации:
Похожие расчеты
Смотрите также
- Делители числа - Список всех делителей числа
- Простое ли число - Узнать, является ли заданное число простым или нет
- Список простых чисел - Список всех простых чисел - сколько простых чисел в диапазоне
<a href="https://calculat.io/ru/number/prime-factors-of/678">Простые множители числа 678 - Calculatio</a>
Таблица разложения чисел на простые множители
| Число | Простые множители |
|---|---|
| 663 | 3, 13, 17 |
| 664 | 23 × 83 |
| 665 | 5, 7, 19 |
| 666 | 2 × 32 × 37 |
| 667 | 23, 29 |
| 668 | 22 × 167 |
| 669 | 3, 223 |
| 670 | 2, 5, 67 |
| 671 | 11, 61 |
| 672 | 25 × 3 × 7 |
| 673 | 673 |
| 674 | 2, 337 |
| 675 | 33 × 52 |
| 676 | 22 × 132 |
| 677 | 677 |
| 678 | 2, 3, 113 |
| 679 | 7, 97 |
| 680 | 23 × 5 × 17 |
| 681 | 3, 227 |
| 682 | 2, 11, 31 |
| 683 | 683 |
| 684 | 22 × 32 × 19 |
| 685 | 5, 137 |
| 686 | 2 × 73 |
| 687 | 3, 229 |
| 688 | 24 × 43 |
| 689 | 13, 53 |
| 690 | 2, 3, 5, 23 |
| 691 | 691 |
| 692 | 22 × 173 |
О калькуляторе "Разложение чисел на простые множители"
Простые множители - это положительные целые числа, имеющие только два делителя - 1 и само себя.