Prime Factorization of 7420
What is the Prime Factorization of 7420?
Answer
or
Explanation of number 7420 Prime Factorization
Prime Factorization of 7420 is expressing 7420 as the product of prime factors. In other words, it is finding which prime numbers should be multiplied together to make 7420.
Since number 7420 is a Composite number (not Prime) we can do its Prime Factorization.
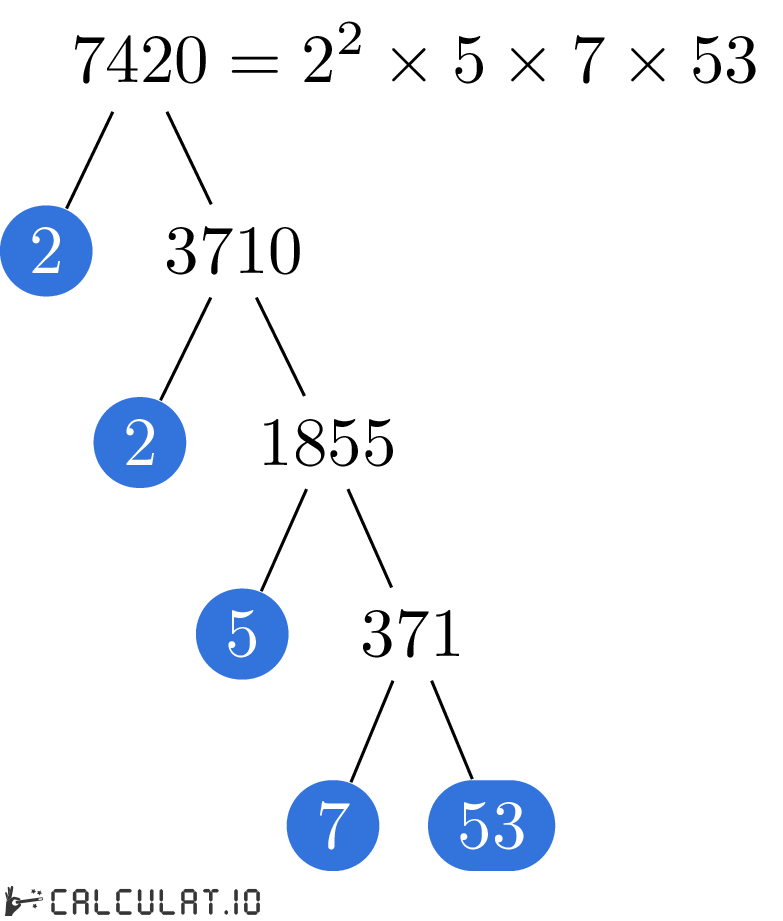
To get a list of all Prime Factors of 7420, we have to iteratively divide 7420 by the smallest prime number possible until the result equals 1.
Here is the complete solution of finding Prime Factors of 7420:
The smallest Prime Number which can divide 7420 without a remainder is 2. So the first calculation step would look like:
7420 ÷ 2 = 3710
Now we repeat this action until the result equals 1:
3710 ÷ 2 = 1855
1855 ÷ 5 = 371
371 ÷ 7 = 53
53 ÷ 53 = 1
Now we have all the Prime Factors for number 7420. It is: 2, 2, 5, 7, 53
Or you may also write it in exponential form: 22 × 5 × 7 × 53
Prime Factor Tree of 7420
We may also express the prime factorization of 7420 as a Factor Tree:
Related Calculations
See Also
- Factors of a Number - List all Factors and Factor Pairs of a Number
- Is a Number Prime - Find out whether a given number is Prime or not
- Prime Numbers List - List of all Prime Numbers - how many Prime numbers are between
<a href="https://calculat.io/en/number/prime-factors-of/7420">Prime factors of 7420 - Calculatio</a>
Prime Factorization Table
| Number | Prime Factors |
|---|---|
| 7405 | 5, 1481 |
| 7406 | 2 × 7 × 232 |
| 7407 | 32 × 823 |
| 7408 | 24 × 463 |
| 7409 | 31, 239 |
| 7410 | 2, 3, 5, 13, 19 |
| 7411 | 7411 |
| 7412 | 22 × 17 × 109 |
| 7413 | 3, 7, 353 |
| 7414 | 2, 11, 337 |
| 7415 | 5, 1483 |
| 7416 | 23 × 32 × 103 |
| 7417 | 7417 |
| 7418 | 2, 3709 |
| 7419 | 3, 2473 |
| 7420 | 22 × 5 × 7 × 53 |
| 7421 | 41, 181 |
| 7422 | 2, 3, 1237 |
| 7423 | 13, 571 |
| 7424 | 28 × 29 |
| 7425 | 33 × 52 × 11 |
| 7426 | 2, 47, 79 |
| 7427 | 7, 1061 |
| 7428 | 22 × 3 × 619 |
| 7429 | 17, 19, 23 |
| 7430 | 2, 5, 743 |
| 7431 | 3, 2477 |
| 7432 | 23 × 929 |
| 7433 | 7433 |
| 7434 | 2 × 32 × 7 × 59 |
About "Prime Factorization" Calculator
Prime factors are the positive integers having only two factors - 1 and the number itself