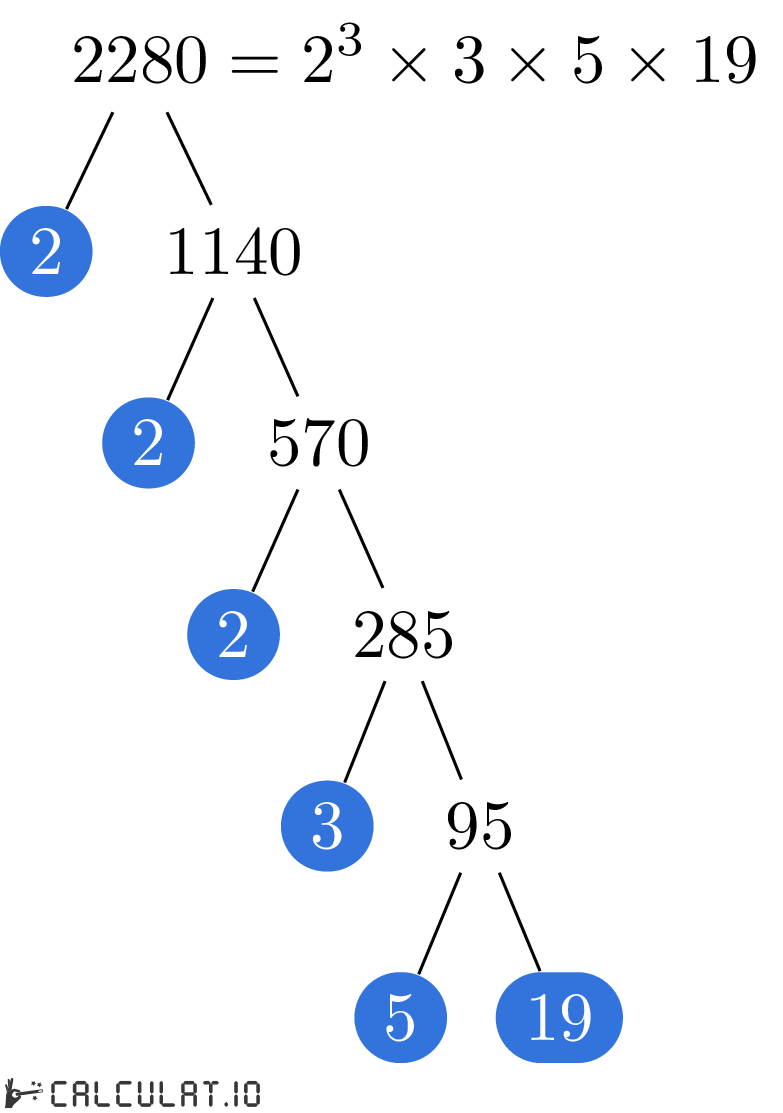
Prime Factorization of 2280
What is the Prime Factorization of 2280?
Answer
or
Explanation of number 2280 Prime Factorization
Prime Factorization of 2280 is expressing 2280 as the product of prime factors. In other words, it is finding which prime numbers should be multiplied together to make 2280.
Since number 2280 is a Composite number (not Prime) we can do its Prime Factorization.
To get a list of all Prime Factors of 2280, we have to iteratively divide 2280 by the smallest prime number possible until the result equals 1.
Here is the complete solution of finding Prime Factors of 2280:
The smallest Prime Number which can divide 2280 without a remainder is 2. So the first calculation step would look like:
2280 ÷ 2 = 1140
Now we repeat this action until the result equals 1:
1140 ÷ 2 = 570
570 ÷ 2 = 285
285 ÷ 3 = 95
95 ÷ 5 = 19
19 ÷ 19 = 1
Now we have all the Prime Factors for number 2280. It is: 2, 2, 2, 3, 5, 19
Or you may also write it in exponential form: 23 × 3 × 5 × 19
Prime Factor Tree of 2280
We may also express the prime factorization of 2280 as a Factor Tree:
Related Calculations
See Also
- Factors of a Number - List all Factors and Factor Pairs of a Number
- Is a Number Prime - Find out whether a given number is Prime or not
- Prime Numbers List - List of all Prime Numbers - how many Prime numbers are between
<a href="https://calculat.io/en/number/prime-factors-of/2280">Prime factors of 2280 - Calculatio</a>
Prime Factorization Table
| Number | Prime Factors |
|---|---|
| 2265 | 3, 5, 151 |
| 2266 | 2, 11, 103 |
| 2267 | 2267 |
| 2268 | 22 × 34 × 7 |
| 2269 | 2269 |
| 2270 | 2, 5, 227 |
| 2271 | 3, 757 |
| 2272 | 25 × 71 |
| 2273 | 2273 |
| 2274 | 2, 3, 379 |
| 2275 | 52 × 7 × 13 |
| 2276 | 22 × 569 |
| 2277 | 32 × 11 × 23 |
| 2278 | 2, 17, 67 |
| 2279 | 43, 53 |
| 2280 | 23 × 3 × 5 × 19 |
| 2281 | 2281 |
| 2282 | 2, 7, 163 |
| 2283 | 3, 761 |
| 2284 | 22 × 571 |
| 2285 | 5, 457 |
| 2286 | 2 × 32 × 127 |
| 2287 | 2287 |
| 2288 | 24 × 11 × 13 |
| 2289 | 3, 7, 109 |
| 2290 | 2, 5, 229 |
| 2291 | 29, 79 |
| 2292 | 22 × 3 × 191 |
| 2293 | 2293 |
| 2294 | 2, 31, 37 |
About "Prime Factorization" Calculator
Prime factors are the positive integers having only two factors - 1 and the number itself